Rezy rotačnej kužeľovej plochy

RNDr. Dagmar Szarková

Obsah:

1. Klasifikácia rezov na kuželi

2. Eliptický rez:

Príklad 1: Rez rotačnej kužeľovej plochy rovinou a, ktorá je kolmá na priemetňu v Mongeovom premietaní.

Príklad 2: Rez rotačnej kužeľovej plochy rovinou a, ktorá je kolmá na pomocnú priemetňu v kolmej axonometrii.

Príklad 3: Rez rotačnej kužeľovej plochy rovinou a, ktorá je vo všeobecnej polohe v Mongeovom premietaní.

3. Parabolický rez

Príklad 4: Rez rotačnej kužeľovej plochy rovinou a, ktorá je kolmá na priemetňu v Mongeovom premietaní.

Príklad 5: Rez rotačnej kužeľovej plochy rovinou a, ktorá je kolmá na pomocnú priemetňu v kolmej axonometrii.

Príklad 6: Rez rotačnej kužeľovej plochy rovinou a, ktorá je vo všeobecnej polohe v Mongeovom premietaní.

4. Hyperbolický rez

Príklad 7: Rez rotačnej kužeľovej plochy rovinou a, ktorá je kolmá na priemetňu v Mongeovom premietaní.

Príklad 8: Rez rotačnej kužeľovej plochy rovinou a, ktorá je kolmá na pomocnú priemetňu v kolmej axonometrii.

Príklad 9: Rez rotačnej kužeľovej plochy rovinou a, ktorá je vo všeobecnej polohe v Mongeovom premietaní.

5. Úlohy na precvičenie

Späť na obsah

1. Klasifikácia rezov na kuželi

Označme pre rotačnú kužeľovú plochu: V - vrchol

o - os

k - určujúcu kružnicu (ležiacu v rovine kolmej os o).

Každú rovinu, ktorá prechádza vrcholom V, budeme nazývať vrcholovou rovinou.

Rezom kužeľovej plochy rovinou je vždy kužeľosečka, a to:

1) singulárna - bod, priamka alebo dve priamky, ak rezová rovina je vrcholová;

2) regulárna - elipsa (špec. kružnica), parabola, hyperbola, ak rovina rezu neprechádza vrcholom V.

Druh regulárnej rezovej kužeľosečky zistíme pomocou vrcholovej roviny rovnobežnej s rezovou rovinou.

Označme: a - rezovú rovinu

s - vrcholovú rovinu, s//a .

a) ak vrcholová rovina má s kužeľovou plochou spoločný iba vrchol V, rezom bude elipsa - obr.1 (špeciálne kružnica, ak rovina a je kolmá na os o) ;

b) ak vrcholová rovina sa dotýka kužeľovej plochy pozdĺž jednej tvoriacej priamky q, rezom bude parabola - obr.4 (os paraboly o’ je rovnobežná s priamkou q) ;

c) ak vrcholová rovina pretína kužeľovú plochu v dvoch tvoriacich priamkach ¹q, ²q, rezom bude hyperbola - obr.7 (asymptoty hyperboly sú rovnobežné s priamkami ¹q, ²q).

Hlavné vrcholy elipsy a hyperboly, resp. vrchol paraboly sú vždy priesečníky spádovej priamky rezovej roviny (pretínajúcej os o) s kužeľovou plochou.

Späť na obsah

2. Eliptický rez

Príklad č.1:

V Mongeovom premietaní zobrazte rez rotačnej kužeľovej plochy, ktorej určujúca kružnica leží v pôdorysni, rovinou a kolmou na nárysňu.

Obr. 1.

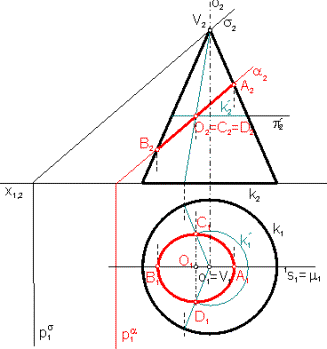
Riešenie - obr.1 :

Vrcholová rovina s má s kužeľovou plochou spoločný iba vrchol - rezová kužeľosečka je elipsa, ktorá sa v náryse zobrazí do úsečky A₂B₂.

Pôdorysy A₁, B₁ hlavných vrcholov elipsy ležia na pôdoryse spádovej priamky ¹s₁ (¹s₁ leží v rovine μ, ktorá je kolmá na rovinu rezu a prechádza osou o) a sú vrcholmi pôdorysu rezovej elipsy. Stred O elipsy je v strede úsečky AB. Vedľajšie vrcholy C, D elipsy sú priesečníky hlavnej priamky p rezovej roviny prechádzajúcej stredom O s kužeľovou plochou. Nájdeme ich na kružnici k’ s polomerom r’, ktorá leží v rovine p’ kolmej na os o a prechádzajúcej bodom O. Vrcholy C₁, D₁ pôdorysu elipsy môžeme odvodiť tiež z druhého priemetu (O₂=C₂=D₂) pomocou obrazov tvoriacich priamok kužeľovej plochy, ktoré prechádzajú bodmi C a D.

Späť na obsah

Pri riešení rezu v kolmej axonometrii je výhodné využiť priemet kužeľovej plochy do tej pomocnej priemetne, na ktorú je rezová rovina kolmá. V pomocnom priemete ľahko určíme druh rezovej kužeľosečky.

Príklad č.2:

V kolmej axonometrii zobrazte rotačnú kužeľovú plochu s určujúcou kružnicou v pôdorysni a jej rez rovinou a kolmou na nárysňu.

Riešenie - obr.2 :

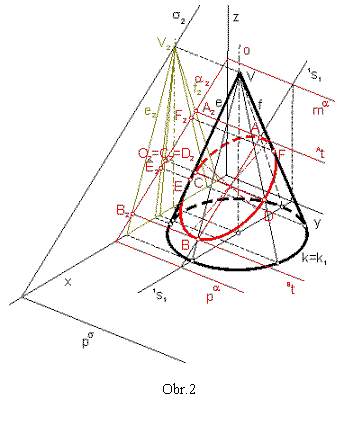
V našom prípade využijeme axonometrický nárys. Vrcholová rovina sa v ňom zobrazí do priamky s₂. Vidíme, že vrcholová rovina obsahuje iba vrchol V, preto rez je elipsa. Axonometrický nárys rezovej čiary je úsečka A₂B₂ z priamky a₂ (do ktorej sa zobrazí rezová rovina) ako v príklade č.1. Axonometrické priemety vrcholov rezovej elipsy A, B, C, D nájdeme pomocou obrazov tvoriacich priamok, ktoré týmito bodmi prechádzajú. Úsečky AB, CD sú združené priemery elipsy, ktorá je obrazom rezu. Pre získanie výsledku využijeme Rytzovu konštrukciu.

Body E, F prechodu pre viditeľnosť hľadáme ako priesečníky obrysových tvoriacich priamok e, f s rezovou rovinou a (najvhodnejšie s využitím pomocného priemetu - v našom prípade - axonometrického nárysu) :

e , f®e₂ , f₂ ,

E₂=e₂Ç a₂ , E₂®E Ů EÎe ,

F₂=f₂Ç a₂ , F₂ ® F Ů FÎf .

Viditeľné body rezovej čiary sú len na viditeľných tvoriacich priamkach.

Späť na obsah

Ak zobrazujeme v Mongeovej projekcii rez rovinou vo všeobecnej polohe, využijeme transformáciu priemetní. Novú priemetňu b zvolíme kolmo na rovinu určujúcej kružnice a rovinu rezu.

Príklad č. 3:

V Mongeovom premietaní zobrazte rez rotačnej kužeľovej plochy, ktorej určujúca kružnica leží v pôdorysni, rovinou a=p^an^a .

Riešenie - obr.3 :

Zvolíme si vhodne novú priemetňu b a zostrojíme 3. priemet roviny a (zobrazí sa ako priamka a₃) a 3. priemet kužeľovej plochy. Rez riešime analogicky ako v príklade č.1, ale tentoraz pracujeme s 1. a 3. priemetom.

Z 3. priemetu vrcholovej roviny je vidieť, že vrcholová rovina obsahuje iba vrchol V, preto rez je elipsa. Jej hlavné vrcholy A, B ležia na spádovej ¹s, preto vieme ľahko priradiť ich jednotlivé priemety (A₃®A₁®A₂, B₃®B₁®B₂). Vedľajšie vrcholy C, D ležia na hlavnej priamke p (C₃®C₁®C₂, D₃®D₁®D₂). AB, CD sú združené priemery elipsy. Pôdorysy ich krajných bodov A₁, B₁, C₁, D₁ sú vrcholmi pôdorysu rezovej elipsy. Nárys elipsy vyrysujeme pomocou Rytzovej konštrukcie zo združených priemerov A₂B₂, C₂D₂.

Body E, F prechodu pre viditeľnosť riešime ako priesečníky obrysových priamok e, (ktoré tvoria hlavný meridián kužeľovej plochy) s rovinou rezu:

e₂®e₁®e₃ ,

E₃=e₃Ça₃ , E₃®E₁®E₂ Ů EÎe ,

f₂®f₁®f₃ ,

F₃=f₃Ça₃ , F₃® F₁®F₂ Ů FÎf .

Body E, F možno získať tiež pomocou hlavnej priamky n (2. osnovy) rezovej roviny ležiacej v rovine hlavného meridiánu.

Viditeľné body rezovej čiary ležia na viditeľných tvoriacich priamkach. V 2. priemete sú viditeľné tie tvoriace priamky, ktoré ležia pred rovinou hlavného meridiánu.

Späť na obsah

3. Parabolický rez

V prípade parabolického rezu treba mať na zreteli, že poloha rezovej roviny je viazaná podmienkou 2)b) z kap.1, čiže rez kužeľovej plochy rovinou je parabola práve vtedy, ak rezová rovina je rovnobežná s niektorou z dotykových rovín danej kužeľovej plochy. Rezová rovina je (okrem spomínanej podmienky) určená priamkou, ktorá v nej leží, najčastejšie jednou stopou. V nasledujúcich príkladoch je zobrazené vždy jedno z dvoch možných riešení.

Príklad č.4:

V Mongeovom premietaní zobrazte parabolický rez rotačnej kužeľovej plochy, ktorej určujúca kružnica leží v pôdorysni, rovinou a=p^a,? .

Obr. 4

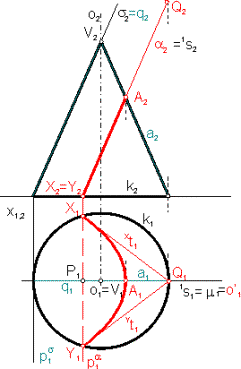
Riešenie - obr.4 :

Najskôr dourčíme rovinu a podľa polohy dotykovej vrcholovej roviny s (a₂//s₂). Parabolický rez sa v náryse zobrazí do úsečky X₂A₂ .

Spádová priamka ¹s je osou o’ paraboly a vrchol A je jej priesečník s kužeľovou plochou. Pôdorys vrchola A je vrcholom pôdorysu rezovej paraboly. Rovina a pretína určujúcu kružnicu k v bodoch X, Y. Parabolu, ktorá je pôdorysom rezu, narysujeme pomocou vety o subtangente (úP₁A₁ú =úA₁Q₁ú, bod Q₁Îk₁). ^Xt=XQ, ^Yt=YQ sú dotyčnice paraboly.

Späť na obsah

Späť na obsah

Príklad č.5:

V kolmej axonometrii zobrazte rotačnú kužeľovú plochu s určujúcou kružnicou v pôdorysni a jej parabolický rez rovinou a=p^a,? .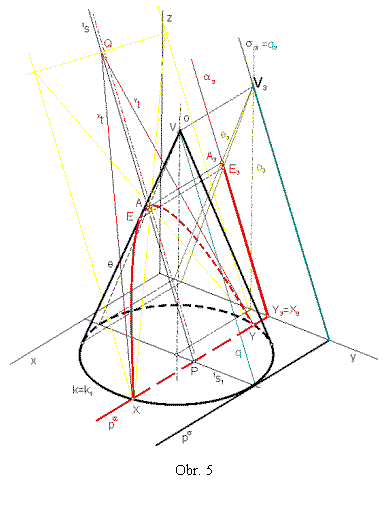

Riešenie - obr.5 :

Pretože rezová rovina je kolmá na bokorysňu, využijeme axonometrický bokorys.

Dourčíme rovinu a podľa polohy dotykovej vrcholovej roviny s (a // s). Obe roviny kolmé na bokorysňu sa zobrazia do priamok a₃, s₃ (a₃ //s₃). Axonometrický bokorys rezovej čiary je úsečka X₃A₃ z priamky a₃, podobne ako v príklade č.4. Axonometrický priemet bodu A odvodíme z jeho axonometrického bokorysu pomocou tvoriacej priamky, ktorá ním prechádza. Bod A je hlavným vrcholom paraboly, ale jeho axonometrický priemet sa nezobrazí do hlavného vrchola obrazu rezu. Body X, Y, ktoré patria rezovej parabole, sú priesečníky roviny a s určujúcou kružnicou k. Os paraboly je spádová priamka ¹s (¹s //q), ale jej axonometrický priemet nie je osou obrazu paraboly (konštrukcia ¹s - viď metrické úlohy v kolmej axonometrii). ¹s možno zostrojiť ako priamku prechádzajúcu bodom A, rovnobežnú s priamkou q, pozdĺž ktorej sa vrcholová rovina dotýka kužeľovej plochy (¹s=PA, kde bod P je stred úsečky XY). Bod Q (Qιs Ů ú QAú = ú APú) je priesečníkom dotyčníc ^Xt=XQ a ^Yt=YQ, axonometrický priemet paraboly je teda jednoznačne určený - ^Xt, X, ^Yt,, Y.

Body E, F prechodu pre viditeľnosť hľadáme podobne ako v príklade č.2, len namiesto axonometrického nárysu použijeme axonometrický bokorys.

Späť na obsah

Príklad č.6:

V Mongeovom premietaní zobrazte parabolický rez rotačnej kužeľovej plochy, ktorej určujúca kružnica leží v pôdorysni, rovinou a=p^a,? .

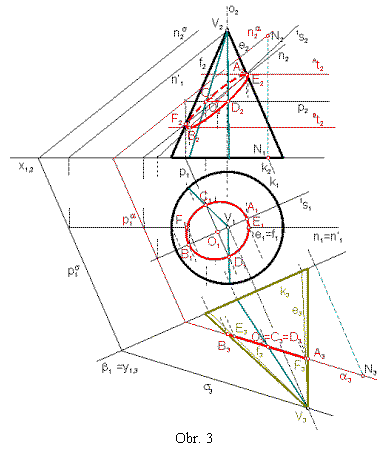
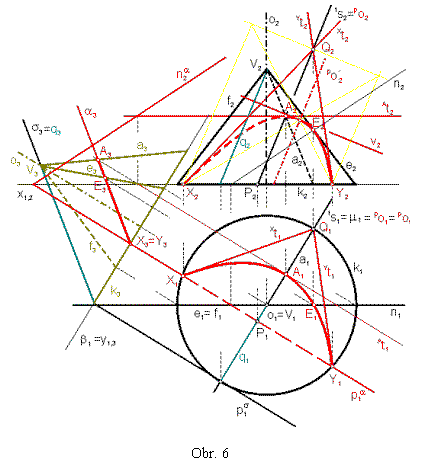Riešenie - obr.6 :

Zvolíme si vhodne novú priemetňu b a zostrojíme 3. priemet kužeľovej plochy a 3. priemet roviny s (zobrazí sa ako priamka s₃) a dourčíme rovinu a. Rez riešime analogicky ako v príklade č.4, ale tentoraz pracujeme s 1. a 3. priemetom.

Úsečka X₃A₃ je tretím priemetom paraboly. Bod A je najvyšším bodom paraboly a leží na spádovej priamke ¹s. Ľahko vieme priradiť priemety bodu A (A₃®A₁®A₂). Pôdorys rezu nájdeme ako v príklade č.4. Bod A₂ nie je vrcholom a ¹s₂ nie je osou priemetu paraboly. Body X, Y ležia na určujúcej kružnici a sú bodmi paraboly.

Bod Qιs, preto ho môžeme ľahko nájsť v 2. priemete buď pomocou ¹s, alebo pomocou hlavnej priamky p rezovej roviny. Nárys paraboly je takto jednoznačne určený dotyčnicami ^Xt₂=X₂Q₂ a ^Yt₂=Y₂Q₂, kde X₂ je dotykový bod dotyčnice ^Xt₂ a Y₂ je dotykový bod dotyčnice ^Yt₂. Takto určenú parabolu vieme narysovať.

Body E, F prechodu pre viditeľnosť riešime ako v príklade č.3 .

Späť na obsah

4. Hyperbolický rez

Hlavné vrcholy A, B hyperboly sú priesečníky spádovej priamky rezovej roviny pretínajúcej os rotácie s kužeľovou plochou. Stred O hyperboly je v strede úsečky AB. Asymptoty ¹as, ²as prechádzajú stedom O a sú rovnobežné s tvoriacimi priamkami ¹q, ²q, v ktorých vrcholová rovina s (s//a) pretína kužeľovú plochu. Pretože nie vždy sú pre nás dostupné oba vrcholy hyperboly, uvedieme ešte ďalší spôsob získania asymptôt:

Pozdĺž tvoriacich priamok ¹q, ²q zostrojíme dotykové roviny ¹t,²t kužeľovej plochy, ktorých stopy p^1t, p^2t (pre kÎp ) sú dotyčnice určujúcej kružnice k v bodoch 1 a 2 (v stopníkoch tvoriacich priamok). Asymptoty ¹as, ²as sú priesečnice rovín ¹t a ²t s rezovou rovinou a (¹as=¹tÇa a ²as=²tÇa). Pretože s//a, je ¹as//¹q a ²as//²q (priesečnice dvoch rovnobežných rovín s treťou rovinou sú navzájom rovnobežné).

Hyperbola prechádza bodmi X a Y, v ktorých rovina a pretína určujúcu kružnicu k.

Rezová hyperbola je teda určená asymptotami a bodom hyperboly.

Späť na obsah

Príklad č.7:

V Mongeovom premietaní zobrazte rez rotačnej kužeľovej plochy, ktorej určujúca kružnica leží v pôdorysni, rovinou a kolmou na nárysňu.

Obr. 7.

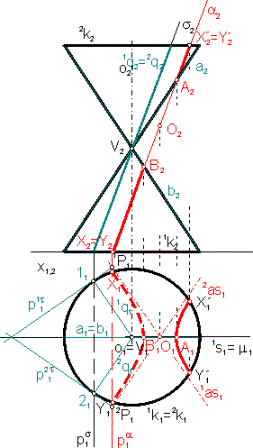
Riešenie - obr.7 :

Vrcholová rovina s//a pretína kužeľovú plochu v dvoch tvoriacich priamkach ¹q,²q - rezová kužeľosečka je hyperbola, ktorá sa v náryse zobrazí do úsečiek X₂A₂ a B₂X’₂ z priamky a₂ .

Pôdorysy A₁, B₁ ležia na pôdoryse spádovej priamky ¹s₁ a sú vrcholmi pôdorysu rezovej hyperboly. Stredom O₁ úsečky A₁B₁ zostrojíme asymptoty ¹as₁,²as₁ rovnobežne s ¹q₁,²q₁. V obrázku č.7 je vyznačená aj konštrukcia asymptôt pomocou dotykových rovín ¹t, ²t :

¹P₁=p^1t₁Çp^a₁ Ů ¹P₁ιas₁ Ů ¹as₁//¹q₁ ,

²P₁= p^2t₁Çp^a₁ Ů ²P₁βas₁ Ů ²as₁//²q₁ .

Teraz už máme dostatok prvkov pre narysovanie pôdorysu hyperboly.

Späť na obsah

Späť na obsah

Príklad č.8:

V kolmej axonometrii zobrazte rotačnú kužeľovú plochu s určujúcou kružnicou v nárysni a jej rez rovinou a kolmou na pôdorysňu.

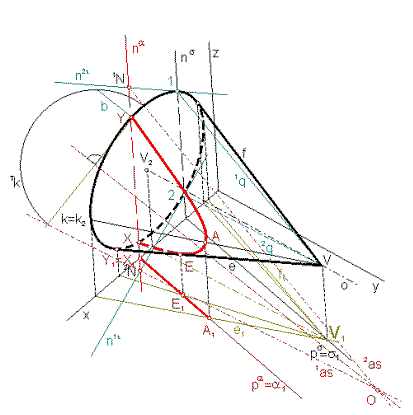Riešenie - obr.8 :

Pretože rezová rovina je kolmá na pôdorysňu, využijeme axonometrický pôdorys.

Vrcholová rovina (ktorá sa v pôdoryse zobrazí do priamky s₁), pretína kužeľovú plochu v dvoch tvoriacich priamkach ¹q,²q - rez je hyperbola. Keďže uvažujeme iba časť kužeľovej plochy medzi určujúcou kružnicou a vrcholom V, zobrazíme iba časť jednej vetvy rezovej hyperboly, ktorej axonometrický pôdorys je úsečka X₁A₁ z priamky a₁ (podobne ako v príklade č.7). Axonometrický priemet vrchola A rezovej hyperboly nájdeme pomocou obrazu tvoriacej priamky, ktorá týmto bodom prechádza. Asymptoty ¹as ,²as zostrojíme ako v príklade č.7, ale pretože určujúca kružnica k leží v nárysni, treba použiť nárysné stopy rovín - n^1t , n^2t :

¹N=n^1t Çn^a Ů ¹Nιas Ů ¹as//¹q ,

²N=n^2t Çn^a Ů ²Nβas Ů ²as//²q .

I keď axonometrický priemet vrchola A hyperboly nie je vrcholom jej priemetu, spolu s priemetmi asymptôt stačí pre narysovanie výsledku.

Body prechodu pre viditeľnosť riešime ako v príklade č.2 .

Späť na obsah

Príklad č.9:

V Mongeovom premietaní zobrazte rez rotačnej kužeľovej plochy, ktorej určujúca kružnica je v pôdorysni, rovinou a=p^a, n^a .

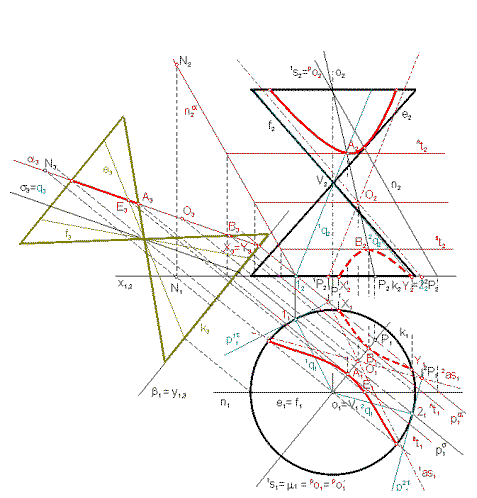
Riešenie - obr.9 :

Zvolíme si vhodne novú priemetňu b a zostrojíme 3. priemet kužeľovej plochy a 3. priemet roviny a (zobrazí sa ako priamka a₃).

V₃Îs₃ Ů s₃//a₃. Vidíme, že vrcholová rovina pretína kužeľovú plochu v dvoch tvoriacich priamkach - rez bude hyperbola. Riešime analogicky ako v príklade č.7, ale tentoraz pracujeme s 1. a 3. priemetom.

Úsečky X₃A₃, B₃X´₃ z priamky a₃ zobrazujú hyperbolu v tomto pomocnom priemete. Body A, B ležia na spádovej priamke ¹s. Ľahko vieme priradiť priemety bodov A a B (A₃®A₁®A₂, B₃®B₁®B₂). Pôdorys rezu nájdeme ako v príklade č.7. Body A₂, B₂ nie sú hlavnými vrcholmi a ¹s₂ nie je hlavnou osou priemetu hyperboly. Nájdeme nárysy asymptôt, ktoré ležia v rovine a (¹as=¹PO, ²as=²PO). Ich prienikom je nárys O₂ stredu hyperboly, ktorý sa dá odvodiť tiež z pôdorysu O₁ pomocou obrazov hlavnej priamky p.

Nárys hyperboly je dostatočne určený asymptotami a bodom hyperboly.

Body prechodu pre viditeľnosť riešime podobne ako v príklade č.3. Z pôdorysu vidieť, že v tomto prípade treba hľadať iba jeden bod prechodu pre viditeľnosť v náryse (pôdorys rezu má jediný spoločný bod s pôdorysom roviny hlavného meridiánu). V našom prípade je v 1. priemete viditeľná iba jedna vetva hyperboly, ktorej body majú z-ové súradnice väčšie ako vrchol V.

5. Cvičenia

1. V Mongeovom premietaní zobrazte rez rotačnej kužeľovej plochy s podstavnou kružnicou k(S,r) ležiacou v pôdorysni rovinou a! [S(0; 5; 0), r=4cm, v=6cm, a(5; Ą; 3 ]

2. V Mongeovom premietaní zobrazte parabolický rez rotačnej kužeľovej plochy s podstavnou kružnicou k(S,r) ležiacou v pôdorysni rovinou a! [S(0; 5; 0), r=4cm, v=6, a(1,5; Ą; ?)]

3. V Mongeovom premietaní zobrazte rez rotačnej kužeľovej plochy (dvojkužeľa) s podstavnou kružnicou k(S,r) ležiacou v pôdorysni rovinou a! [S(0; 5; 0), r=4cm, v=6cm, a(-6; Ą; 3)]

4. V Mongeovom premietaní zobrazte rez rotačnej kužeľovej plochy s podstavnou kružnicou k(S,r) ležiacou v pôdorysni rovinou a! [S(0; 4; 0), r=3cm, v=5cm, a(8; 9; 4)]

5. V Mongeovom premietaní zobrazte parabolický rez rotačnej kužeľovej plochy s podstavnou kružnicou k(S,r) ležiacou v pôdorysni rovinou a! [S(0; 5; 0), r=4cm, v=8cm, a(-4,5; 3,5; ?)]

6. V Mongeovom premietaní zobrazte rez rotačnej kužeľovej plochy (dvojkužeľa) s podstavnou kružnicou k(S,r) ležiacou v pôdorysni rovinou a! [S(-4; 5; 0), r=4cm, v=5cm, a(-3 ; -2,5; 4)]

7. V kolmej axonometrii (XY=10cm, XZ=11cm, YZ=12cm) zobrazte rez rotačnej kužeľovej plochy s podstavnou kružnicou k(S,r) a výškou v, rovinou a! [kĚ n, S(5; 0; 4), r=4,5cm, v=10cm, a(Ą; 7,5; 11)]

8. V kolmej axonometrii (XY=10cm, XZ=11cm, YZ=12cm) zobrazte parabolický rez rotačnej kužeľovej plochy s podstavnou kružnicou k(S,r) a výškou v, rovinou a! [kĚ m, S(0; 6; 5), r=4,5cm, v=11cm, a(?; Ą; 6)]

9. V kolmej axonometrii (XY=10cm, XZ=11cm, YZ=12cm) zobrazte rez rotačnej kužeľovej plochy (dvojkužeľa) s podstavnou kružnicou k(S,r) a výškou v, rovinou a! [kĚ p, S(5; 1; 0), r=5cm, v=7cm, a(3; Ą; Ą)]

Späť na obsah

Posledná zmena: 12. februára 2000