Vektory a matice - základy

Príklad 1. Matice sú v systéme Mathematica prezentované ako dvojrozmerné zoznamy riadkov. Zobrazíme ich pomocou štandardných príkazov, alebo pomocou paliet symbolov. Maticu m násobíme číslom 3. Vypočítaný je tiež súčet matíc m a m1.

m={{a,b},{c,d}}
3m

{{a, b}, {c, d}}

{{3 a, 3 b}, {3 c, 3 d}}

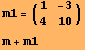
m1 = (1 -3) 4 10 m + m1

{{1, -3}, {4, 10}}

{{1 + a, -3 + b}, {4 + c, 10 + d}}

Príklad 2. Pomocou funkcie TableForm alebo MatrixForm zobrazíme matice v štandardnom tvare:

u={{1,2},{0,1}};  
TableForm[%]
MatrixForm[u]
v={{3,1},{2,2}};  
TableForm[%]

1 2
0 1

( 1 2 ) 0 1

3 1
2 2

Príklad 3. Súčin matíc označujeme symbolom . (bodka). Funkcia element[[ ]] zobrazí definovaný prvok matice, v prvom riadku a druhom stĺpci .

pr=u.v
MatrixForm[%]
element=%[[1,2]]

{{7, 5}, {2, 2}}

( 7 5 ) 2 2

5

Príklad 4. Súčin matice m a vektora {x, y}:

m
r= m.{x,y}  
{x,y} .m
MatrixForm[r]

{{a, b}, {c, d}}

{a x + b y, c x + d y}

{a x + c y, b x + d y}

( a x + b y ) c x + d y

Príklad 5. Mnoho špeciálnych funkcií umožňuje výpočet rôznych charakteristík matíc, konkrétnych typov matíc a vektorov, a pod. Napr. počet prvkov udáva funkcia Length, postupnosť za sebou nasledujúcich čísel vytvorí funkcia Range.

s1=Table[Exp[x],{x,0,1,0.25}]
Length[s1]    (* Gives the number of elements in the list *)
r6=Range[6]
Range[3,7]     (* Gives a list, containing the consecutive numbers from 3 to 7  *)
Range[3,7,0.5] (* The same, but with a step 0.5  *)

RowBox[{{, RowBox[{1, ,, 1.28403, ,, 1.64872, ,, 2.117, ,, 2.71828}], }}]

5

{1, 2, 3, 4, 5, 6}

{3, 4, 5, 6, 7}

RowBox[{{, RowBox[{3, ,, 3.5, ,, 4., ,, 4.5, ,, 5., ,, 5.5, ,, 6., ,, 6.5, ,, 7.}], }}]

Príklad 6. Štandardne postupnosti vytvárame pomocou funkcie Array.  Vymažeme aktuálne hodnoty premenných, aby sme sa vyhli chybám.

Clear[a,b,x,y]
Array[a,4]

{a[1], a[2], a[3], a[4]}

Príklad 7. Niekoľko ďalších príkladov formálnych postupností - vektorov a matíc:

Array[b,{4,1}]
MatrixForm[%]
Array[d,{3,3}]
d2=%
MatrixForm[d2]

{{b[1, 1]}, {b[2, 1]}, {b[3, 1]}, {b[4, 1]}}

( b[1, 1] ) b[2, 1] b[3, 1] b[4, 1]

{{d[1, 1], d[1, 2], d[1, 3]}, {d[2, 1], d[2, 2], d[2, 3]}, {d[3, 1], d[3, 2], d[3, 3]}}

{{d[1, 1], d[1, 2], d[1, 3]}, {d[2, 1], d[2, 2], d[2, 3]}, {d[3, 1], d[3, 2], d[3, 3]}}

( d[1, 1] d[1, 2] d[1, 3] ) d[2, 1] d[2, 2] d[2, 3] d[3, 1] d[3, 2] d[3, 3]

Príklad 8. Jednotkovú maticu ľubovoľného rádu, napr. 4, získame veľmi jednoducho.

id=IdentityMatrix[4]
MatrixForm[id]

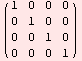
{{1, 0, 0, 0}, {0, 1, 0, 0}, {0, 0, 1, 0}, {0, 0, 0, 1}}

( 1 0 0 0 ) 0 1 0 0 0 0 1 0 0 0 0 1

Príklad 9. Vytvorenie diagonálnej matice a zistenie rozmerov matice.

DiagonalMatrix[Range[4]]
MatrixForm[%]
Dimensions[%]
Dimensions[m]

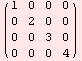
{{1, 0, 0, 0}, {0, 2, 0, 0}, {0, 0, 3, 0}, {0, 0, 0, 4}}

( 1 0 0 0 ) 0 2 0 0 0 0 3 0 0 0 0 4

{4, 4}

{2, 2}

Príklad 10. Jednoduchá definícia diagonálnej matice.

DiagonalMatrix[{-1,2,-3}]
MatrixForm[%]

{{-1, 0, 0}, {0, 2, 0}, {0, 0, -3}}

( -1 0 0 ) 0 2 0 0 0 -3

Príklad 11. Usporiadanie prvkov a iné transformácie.

k1={2,5,6,-2,4,4,1}
k2=Sort[k1]
x=. (*  Clear the current values and definitions of x and a *)
a=.
a=Table[x^(i+j),{i,0,2},{j,0,2}] (* Creating new matrix a by function Table *)
MatrixForm[a]

{2, 5, 6, -2, 4, 4, 1}

{-2, 1, 2, 4, 4, 5, 6}

{{1, x, x^2}, {x, x^2, x^3}, {x^2, x^3, x^4}}

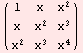
( 2 ) 1 x x 2 3 x x x 2 3 4 x x x

Príklad 12. Výpočet determinantov.

f={{5,3},{4,2}}; MatrixForm[f]
Det[f]

( 5 3 ) 4 2

-2

Príklad 13. Derivácie matice.

a ∂_x a

{{1, x, x^2}, {x, x^2, x^3}, {x^2, x^3, x^4}}

{{0, 1, 2 x}, {1, 2 x, 3 x^2}, {2 x, 3 x^2, 4 x^3}}

a
D[a,x]

{{1, x, x^2}, {x, x^2, x^3}, {x^2, x^3, x^4}}

{{0, 1, 2 x}, {1, 2 x, 3 x^2}, {2 x, 3 x^2, 4 x^3}}

Created by Mathematica  (December 21, 2007)