Matice
úvod, zápis, transformácie, determinanty, inverzné matice, vlastné čísla, riešenie systémov rovníc, atď.
Použitie File/Palettes/Basic Calculations/ List a Matrices menu

Príklad 1. Matice sú v systéme Mathematica reprezentované dvoma spôsobmi - ako štandardné multidimenzionálne zoznamy, alebo pomocou matematickej symboliky použitím paliet. Uvedený je zápis matice a s rozmermi 3 x 5:

a = {{0, 2, 3, 1, 9}, {-2, 1, 0, 0, 3}, {12, 4, 0, -9, 2}}   (* This is a list *) MatrixForm[%]

{{0, 2, 3, 1, 9}, {-2, 1, 0, 0, 3}, {12, 4, 0, -9, 2}}

( 0 2 3 1 9 ) -2 1 0 0 3 12 4 0 -9 2

Nasledujúca matica b je vytvorená použitím symbolu ( )   z palety hlavných symbolov. Riadky sa pridávajú umiestnením kurzora do hornej časti bunky a súčasným stlačením klávesníc CTRL a ENTER. Stĺpec pridáme súčasným stlačením klávesníc CTRL a čiarka - , .

b = (1 0 0 2 3) 1 2 0 3 5 3 8 3 1 6

{{1, 0, 0, 2, 3}, {1, 2, 0, 3, 5}, {3, 8, 3, 1, 6}}

Príklad 2. Operácie s maticami sa vykonávajú podľa pravidiel lineárnej algebry - súčet, súčin, atď. Uvedený je súčet a súčin matice a čísla.

c = 5a ; MatrixForm[%] d = 4a - 10b ; MatrixForm[%]

( 0 10 15 5 45 ) -10 5 0 0 15 60 20 0 -45 10

( -10 8 12 -16 6 ) -18 -16 0 -30 -38 18 -64 -30 -46 -52

Príklad 3. Súčin matíc definuje symbol   .  (bodka):

a1 = (2 0 ) ; 1 -2 9 1 b1 = (1 2 -2 0 ) ; 3 4 0 1 c1 = a1 . b1 ; MatrixForm[%]

( 2 4 -4 0 ) -5 -6 -2 -2 12 22 -18 1

Príklad 4.  Výpočet  (p+q). (p-q). Na porovnanie získaného výsledku vypočítame aj medzivýsledky.

p = (1 2) ; 0 3 q = (0 2) ; 1 0 p + q ; MatrixForm[%] p - q ; MatrixForm[%] (p + q) . (p - q) ; MatrixForm[%]

( 1 4 ) 1 3

( 1 0 ) -1 3

( -3 12 ) -2 9

Príklad 5. Determinanty, transpozícia, umocňovanie, atď. Operácia a^3 vykoná umocnenie každého prvku matice na tretiu, zatiaľ čo operácia a.a.a dáva trojnásobný súčin matice a.

a = (2 3 0) ; 0 1 4 1 2 5 determinanta = Det[a] Transpose[a] ; MatrixForm[%] MatrixPower[a, 3] a . a . a a^3 MatrixForm[%]

6

( 2 0 1 ) 3 1 2 0 4 5

{{20, 45, 96}, {32, 69, 156}, {47, 102, 225}}

{{20, 45, 96}, {32, 69, 156}, {47, 102, 225}}

{{8, 27, 0}, {0, 1, 64}, {1, 8, 125}}

( 8 27 0 ) 0 1 64 1 8 125

Príklad 6. Výpočet inverznej matice a overenie výpočtu pomocou súčinu pôvodnej matice a a inverznej matice r zľava aj sprava, ktorých výsledkom je jednotková matica.

r=Inverse[a]
MatrixForm[%]
a.r
r.a

{{-1/2, -5/2, 2}, {2/3, 5/3, -4/3}, {-1/6, -1/6, 1/3}}

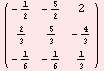
( 1 5 ) -- -- 2 2 2 2 5 ... - -- 3 3 3 1 1 1 -- -- - 6 6 3

{{1, 0, 0}, {0, 1, 0}, {0, 0, 1}}

{{1, 0, 0}, {0, 1, 0}, {0, 0, 1}}

Príklad 7. Zistenie hodnosti matice eliminačnou metódou pomocou funkcie RowReduce.

a = (2 3 7 ) ; 2 3 7 12 3 7 4 3 7 RowReduce[a] ; MatrixForm[%]

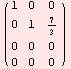
( ) 1 0 0 7 - 0 1 3 0 0 0 0 0 0

Príklad 8. Výpočet vlastných čísel a vlastných vektorov štvorcovej matice, ak existuje analytické riešenie charakteristickej rovnice. V opačnom prípade treba použiť metódu numerického výpočtu.

b=.
b={{3,1},{4,0}}
Eigenvalues[b]
Eigenvectors[b]
c={{1,0,-3},{4,0,-2},{2,-2,3}}
Eigenvalues[c]
Eigenvectors[c]

{{3, 1}, {4, 0}}

{4, -1}

{{1, 1}, {-1, 4}}

{{1, 0, -3}, {4, 0, -2}, {2, -2, 3}}

{4,  5^(1/2), - 5^(1/2)}

{{-2, -3, 2}, {1/2 + ( 5^(1/2))/2, 2, 1}, {1/2 - ( 5^(1/2))/2, 2, 1}}

Príklad 9. Riešenie sústavy lineárnych rovníc Ax = b s nesingulárnou maticou A. Dva spôsoby nájdenia riešenia - priamym výpočtom inverznej matice, x = A^(-1) b  , alebo pomocou funkcie LinearSolve[ ] .

A = (1 4 -4 0.4 1.6 ) ; 0.02 3.5 13 13.04 -44 ... cation of the accurace of the inverse matrix *) ; MatrixForm[%] x1 = r . b x2 = LinearSolve[A, b]

345305.

RowBox[{{, RowBox[{RowBox[{{, RowBox[{0.0279732, ,, 0.00504037, ,, 0.00460558, ,, RowBox[{-, 0 ... 0.0214666}], ,, RowBox[{-, 0.00892012}], ,, 0.00968367, ,, 0.0594927, ,, 0.000474677}], }}]}], }}]

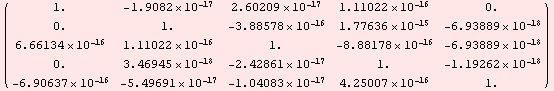
( 0.9999999999999999` -1.9081958235744878`*^-17 2.6020852139652106`*^-17 ... 3`*^-16 -5.4969050145015075`*^-17 -1.0408340855860843`*^-17 4.2500725161431774`*^-16 1.`

RowBox[{{, RowBox[{RowBox[{{, 0.151366, }}], ,, RowBox[{{, RowBox[{-, 0.582198}], }}], ,, RowBox[{{, RowBox[{-, 0.89788}], }}], ,, RowBox[{{, 0.866033, }}], ,, RowBox[{{, 0.149681, }}]}], }}]

RowBox[{{, RowBox[{RowBox[{{, 0.151366, }}], ,, RowBox[{{, RowBox[{-, 0.582198}], }}], ,, RowBox[{{, RowBox[{-, 0.89788}], }}], ,, RowBox[{{, 0.866033, }}], ,, RowBox[{{, 0.149681, }}]}], }}]

Created by Mathematica  (December 21, 2007)