Analýza1

Analýza: derivácie, integrály a limity

Príklad 1. Definujeme polynomickú funkciu premennej x a nájdeme jej prvú a tretiu deriváciu.

f=x^5-2x^3-1
D[f,x]
D[f,{x,3}]

Tie isté príkazy sa dajú zapísať pomocou palety matematických symbolov. Zápis f' vykoná substitúciu. Výpočet derivácie môžeme zabezpečiť symbolmi . V symbole pre tretiu deriváciu pridáme príslušný počet x :

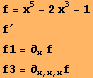
f = x^5 - 2x^3 - 1 f^′ f1 = ∂_x f f3 = ∂_ (x, x, x) f

Týmto spôsobom môžeme deklarovať ľubovoľnú funkciu:

h[x_] := x^5 - 2x^3 - 1 ∂_x h[x] h[1]

Príklad 2. Zobrazíme grafy funkcií z príkladu 1. Priebeh funkcie je zaujímavý na intervale [-2, 2], preto grafy derivácií zobrazíme iba na tomto intervale.

g1 = Plot[f, {x, -5, 5}] g2 = Plot[f1, {x, -2, 2}] g3 = Plot[f3, {x, -2, 2}]

[Graphics:HTMLFiles/index_14.gif]

[Graphics:HTMLFiles/index_16.gif]

[Graphics:HTMLFiles/index_18.gif]

Príklad 3. Definujeme funkciu dvoch premenných a nájdeme jej parciálne derivácie podľa premennej x, potom podľa premennej y a napokon druhú zmiešanú parciálnu deriváciu .

g[x_, y_] := 7x^2 - y^3 - Log[x] ∂_x g[x, y] ∂_y g[x, y] ∂_ (x, y) g[x, y]

Príklad 4. Vynulujeme premennú f. Definujeme symbolickú deriváciu.

f = .
D[f[x],x]
D[5* x *f[x], x]

Príklad 5. Premennej f priradíme novú hodnotu, pričom stará sa vymaže automaticky. Vypočítame neurčitý integrál z f - pomocou symbolov z palety, aj zápisom príkazovej funkcie, a napokon vypočítame určitý integrál funkcie f na danom intervale a vyjadríme jeho číselnú hodnotu.

f = (1 - 2x^3)/(2 + 3x) ∫fxIntegrate[f, x] &nb ... (* Here the symbol % takes the preceding result *)

Príklad 6. Definujeme funkciu dvoch premenných s názvom newf. Vypočítame jej deriváciu podľa premennej x a dvojný integrál na danej oblasti.

newf[x_, y_] := x^4 + 3y d = ∂_x newf[x, y] ∫_0^1∫_1^2newf[x, y] yx %//N

Príklad 7. Definujeme trigonometrickú funkciu. Chceme vypočítať určitý integrál na danej oblasti, ale systém má problémy a výpočet je veľmi pomalý, funkcia cos[ x/y] nie je definovaná v bode y = 0. Zdĺhavé výpočty môžeme prerušiť súčasným stlačením klávesníc ALT + , alebo pomocou Kernel/Abort Evaluation menu.

f=. f[x_, y_] := Cos[( x)/y] ∫_0^π∫_0^πf[x, y] xy ... , π}] (* Approximate integration by numerical method *)

NIntegrate :: slwcon : Numerical integration converging too slowly; suspect one of the followi ... r integrand is oscillatory try using the option Method->Oscillatory in NIntegrate. More…

Príklad 8. Zobrazíme graf funkcie z predchádzajúceho príkladu, aby sme zistili, kde nastávajú singularity.

Plot3D[f[x,y],{x,0,1},{y,0,1}]

[Graphics:HTMLFiles/index_60.gif]

Príklad 9. Definujeme novú funkciu a vypočítame jej dvojný integrál na oblasti, ktorej hranice vzhľadom na y sú určené ako funkcie premennej x.

f=. ; f = x^2 + 1/(1 + y^2) ∫_0^1∫_0^x^(1/2) fyx N[%]

Príklad 10. Príklad trojného integrálu - najprv určíme jeho exaktnú hodnotu, potom vypočítame približnú numerickú hodnotu výsledku s dvojnásobnou presnosťou.

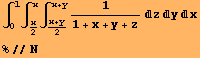
∫_0^1∫_x/2^x∫_ (x + y)/2^(x + y) 1/(1 + x + y + z) zyx %//N

Predchádzajúci výpočet sa dá zapísať aj v štandarnej forme, ako:

f= 1/(1+x+y+z)
Integrate[f,{x,0,1},{y,x/2,x},{z,(x+y)/2,x+y}]
N[%]

Príklad 11. Vyšetrujme teraz inú funkciu. Systém zobrazí jej graf na intervale [0, 10] napriek tomu, že funkcia nie je v bode x = 0 definovaná. Pri zobrazení na väčšom intervale však už graf nie je nakreslený v okolí bodu 0.

f = Sin[x]/x Plot[f, {x, 0, 10}] Plot[f, {x, 0, 100}]