Algoritmy v systéme Mathematica      

Systém Mathematica poskytuje obrovský výber rôznych zabudovaných algoritmov pre exaktné a približné výpočty a riešenia problémov. Najväčšiu skupinu tvoria numerické výpočty koreňov rovníc a systémov rovníc, maticová inverzia , vlastné čísla matice, problémy z teórie čísel, numerická a symbolická integrácia, riešenie diferenciálnych rovníc, a pod.
Ak nie je k dispozícii vhodná zabudovaná funkcia pre riešenie problému, môžeme sa pokúsiť vyhľadať štandardné prídavné balíky systému Mathematica, alebo naprogramovať svoj vlastný algoritmus použitím príkazov vlastného programovacieho jazyka systému Mathematica.

Príklad 1. Zabudovaná funkcia pre riešenie transcendentných rovníc, Newtonova metóda . V uvedenom príklade vypočítame reálne korene rovnice cos x = x + Log x, použitím začiatočného odhadu x = 1. Výhodné je použiť grafickú interpretáciu pre korektný odhad intervalu obsahujúceho riešenie.

FindRoot[Cos[x] == x + Log[x], {x, 1}]

RowBox[{{, RowBox[{x, , 0.840619}], }}]

Zobrazíme graf funkcie f(x) a odhadneme hodnotu premennej, v ktorej funkcia nadobúda hodnotu 0. Riešenie sa nachádza v intervale [0,1]. Niekedy funkcia FindRoot vyžaduje presnejší prvý odhad.

f = Cos[x] - x - Log[x] g1 = Plot[f, {x, 0, 5}]

-x + Cos[x] - Log[x]

[Graphics:HTMLFiles/index_5.gif]

⁃Graphics⁃

Príklad 2. Približné riešenie rovníc a systémov rovníc, v reálnej aj komplexnej rovine. Presné riešenia získame pomocou príkazu Solve[ ]. Ak touto cestou nedospejeme k výsledku, pokúsime sa získať ho pomocou príkazov so zabudovanými algoritmami pre numerické riešenie: NSolve[ ],  FindRoot[ ], Reduce[ ] a inými funkciami. Riešením rovnice piateho stupňa v komplexnej rovine s presnosťou na 30 platných cifier dostávame výstup v tvare zoznamu koreňov, pričom v tomto prípade získame päť reálnych čísel.

x=. NSolve[x^5 - 6x^3 + 8x + 1 == 0, x, 30]

RowBox[{{, RowBox[{RowBox[{{, RowBox[{x, , RowBox[{-, 2.05410715179010988179280712936} ... 9719563865}], }}], ,, RowBox[{{, RowBox[{x, , 1.9215959613089628890382661792}], }}]}], }}]

Príklad 3. Ak chceme vybrať niektorý z koreňov, použijeme nasledujúce zápisy (vyberáme druhý a posledný koreň):

x2 = x/.%[[2]] x5 = x/.%%[[5]]

RowBox[{-, 1.29150071151659313075725844912}]

1.9215959613089628890382661792

Príklad 4. Výpočet približnej hodoty určitého integrálu. Veľé písmeno 'N' uvedené pred funkciou Integrate označuje, že hodnota integrálu je vypočítaná približnou numerickou metódou.
Zápisy v oboch riadkoch sú korektné a dávajú rovnaký výsledok. Ťuknutím na riadok s výstupom a stačením klávesy ENTER sa výsledok zobrazí s presnosťou na 16 desatinných miest.

NIntegrate[Log[x + Sin[x]], {x, 0, 2}] N[∫_0^2Log[x + Sin[x]] x]

0.555889

0.555889

0.555889

Príklad 5. Rozklad prirodzeného čísla na súčin prvočísel. Výsledok sa zobrazuje ako zoznam, v ktorom je ako prvé číslo uvedený prvočiniteľ z rozkladu a za ním jeho exponent.
Prvý výsledok je   18 = 2^13^2, alebo  2.9 = 18.
Druhý výsledok znamená, že číslo n = 172872 sa dá rozložiť na súčin prvočiniteľov v tvare 2^3 3^2 7^4.

FactorInteger[18] n = 172872 ; FactorInteger[n]

{{2, 1}, {3, 2}}

{{2, 3}, {3, 2}, {7, 4}}

Príklad 6. Ku danej štvorcovej matici a sytém nájde inverznú maticu b. Tretia matica c demonštruje dôkaz, že súčinom matíc a . b dostaneme jednotkovú maticu.

a = {{1, -3, 8}, {3, 9, 4}, {-3, 0, 4}} ; MatrixForm[%] b = Inverse[a] ; MatrixForm[%] c = a . b ; MatrixForm[c]

( 1 -3 8 ) 3 9 4 -3 0 4

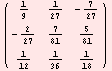
( 1 1 7 ) - -- --- 9 27 27 ... 27 81 81 1 1 1 -- -- -- 12 36 18

( 1 0 0 ) 0 1 0 0 0 1

Príklad 7. Mathematica nájde riešenie diferenciálnej rovnice alebo sústavy rovníc, a to symbolicky (ak je to možné) aj numericky. Nelineárna obyčajná diferenciálna rovnica druhého rádu so začiatočnými podmienkami v bode 0.
                 x'' + x^3 = sin(t),    x(0) = 0,   x'(0) = 0,   t je z intervalu [0, 20].
Algoritmus aproximácie použijeme pomocou funkcie NDSolve. Numerickým riešením dostaneme tabuľku hodnôt, ktorú si systém zapamätá ako interpolačnú funkciu. Výsledok môžeme aj graficky zobraziť.

NDSolve[ {x''[t] + x[t]^3 == Sin[t], x[0] == x '[0] == 0}, <br />      ... nbsp;             x, {t, 0, 20} ]

RowBox[{{, RowBox[{{, RowBox[{x, , TagBox[RowBox[{InterpolatingFunction, [, RowBox[{Ro ... wBox[{{, RowBox[{0., ,, 20.}], }}], }}], ,, <>}], ]}], False, Editable -> False]}], }}], }}]

ParametricPlot[Evaluate[{x[t], x '[t]}/.%], {t, 0, 20}]

[Graphics:HTMLFiles/index_31.gif]

⁃Graphics⁃

Príklad 8. Mathematica rieši aj nerovnice a riešenie sa dá zobraziť graficky. Potrebné algoritmy sú súčasťou špeciálnych balíkov. V tomto príklade vyriešime algebrický systém dvoch nerovníc. Aby sme zamedzili opätovnému použitiu premenných, najprv vynulujeme hodnoty používaných premenných x, y a t pomocou funkcie Clear[ ]. V druhom riadku aktivujeme špeciálny prídavný balík.

Clear[x, y, t] <<Algebra`InequalitySolve`

Nižšie použitý symbol && označuje logický operátor AND a symbol || označuje logický operátor OR.

InequalitySolve[(1 - Abs[2x])/( x - 2) ≥1 && ( 1)/(x - 3) < -x, x]

x≤ -3

Príklad 9. Riešenie systému dvoch nerovníc v rovine.

InequalitySolve[x^2 + y^2<1&&x<y, {x, y}]

-1<x≤ -1/2^(1/2) && -(1 - x^2)^(1/2) <y< (1 - x^2)^(1/2) || -1/2^(1/2) <x<1/2^(1/2) &&x<y< (1 - x^2)^(1/2)

Príklad 10. Riešenie z príkladu 9 môžeme aj graficky zobraziť. Použijeme špeciálny grafický balík.

<<Graphics`InequalityGraphics` InequalityPlot[x^2 + y^2<1&&x<y,    {x, -1, 1}, {y, -1, 1} ] ;

[Graphics:HTMLFiles/index_39.gif]

Created by Mathematica  (October 6, 2007)