Mathematica ako kalkulačka                               

Systém Mathematica sa dá používať ako obyčajná kalkulačka - napíšte výraz, stlačte SHIFT + ENTER   a  systém Mathematica vykoná výpočet a zobrazí výsledok.
V uvedených príkladoch sú podčiarknuté inštrukcie potrebné pre prácu v systéme.

Príklad 1. Umocnenie čísla 3 na druhú. Môžete použiť aj svoje vlastné hodnoty. Na konci príkazového riadku vpravo sa zobrazuje modrá hranatá zátvorka označujúca bunku.
Ked v aktívnej bunke kurzor bliká, stlačte súčasne klávesy    SHIFT+ENTER . Kedykoľvek sa môžete vrátiť späť a nanovo vyhodnotiť ľubovoľnú vybranú bunku.  

3^2

9

Mathematica automaticky pracuje s najväčšou možnou presnosťou výpočtu, napr. 3 umocnené na 100 je číslo so 48 ciframi:

3^100

515377520732011331036461129765621272702107522001

Matematické symboly vyberáme podobne ako v textovom editore MS Word priamo z ponúknutej palety. Predchádzajúci príklad môžeme zapísať výberom z menu: File \ Palettes \ BasicInput v tvare:

3^100

515377520732011331036461129765621272702107522001

Príklad 2. Na uloženie hodnôt, grafov, zoznamov alebo iných objektov systému Mathematica používame premenné.
Pri pomenovaní premenných musíme byť veľmi opatrní, pretože systém rozlišuje veľké a malé písmená abecedy.   Premené A1 a a1 môžu označovať rozličné objekty:

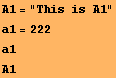
A1 = "This is A1" a1 = 222 a1 A1

This is A1

222

222

This is A1

Príklad 3. Do jednej bunky môžeme umiestniť dva alebo viac výrazov, ktoré sa budú vyhodnocovať jeden po druhom. Skalárny súčin dvoch vektorov a a b, ktorých súradnice sú zapísané v krútených zátvorkách, je vypočítaný a uložený v premennej c. Symbolom skalárneho súčinu je bodka, ktorú je potrebné zapísať, aby sa súčin vykonal.

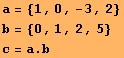
a = {1, 0, -3, 2} b = {0, 1, 2, 5} c = a . b

{1, 0, -3, 2}

{0, 1, 2, 5}

4

Príklad 4. Štandardné matematické konštanty a zabudované funkcie sa označujú veľkými písmenami a argument je uvedený v hranatých zátvorkách.
Systém Mathematica rozlišuje malé a veľké písmená!   Pre zápis môžeme použiť aj palety symbolov a funkcií.

Cos[Pi/4] Tan[π/3]

1/2^(1/2)

3^(1/2)

Príklad 5. Ak cheme získať výsledok v tvare desatinného čísla, stačí aspoň jeden z argumentov zapísať ako desatinné číslo, napr.  2.0,  -12.456,   100.  a pod. Všimnite si rozdiel v zápise výsledku:

Sin[π/12] RowBox[{Sin, [, RowBox[{π, /, 12.}], ]}]

(-1 + 3^(1/2))/(2 2^(1/2))

0.258819

Príklad 6. Matematické výrazy sa zapisujú pomerne jednoducho. Ak je použitým pemenným priradená v predchádzajúcom výpočte nejaká hodnota, Mathematica bude pracovať s touto číselnou hodnotou, v opačnom prípade bude pracovať s príslušným symbolom. Vyriešme najprv kvadratickú rovnicu a potom iracionálnu rovnicu s parametrom k.
V príkaze pre výpočet koreňov rovnice sa používa symbol pre logické porovnanie = = , nie štandardný symbol =.

Solve[5x^2 - 6x + 1 == 0, x]

{{x1/5}, {x1}}

Výsledok môžeme uložiť do pamäte a použiť neskôr. Znak /. je symbolom dosadzovacieho operátora. Znak % použije výsledok výpočtu z predchádzajúceho vykonaného príkazu.

x1 = x/. %[[1]] x2 = x/. %%[[2]]

1/5

1

Solve[x^(1/2) + k == 2x, x] x3 = x/. %[[1]] x4 = x/. %%[[2]]

{{x1/8 (1 + 4 k - (1 + 8 k)^(1/2))}, {x1/8 (1 + 4 k + (1 + 8 k)^(1/2))}}

1/8 (1 + 4 k - (1 + 8 k)^(1/2))

1/8 (1 + 4 k + (1 + 8 k)^(1/2))

Príklad 8. Vypočítajme neurčitý integrál pomocou symbolu, ktorý vyberieme z palety matematických symbolov File \ Palettes \ BasicInput. Ak chceme použiť premennú a ako parameter, musíme zrušiť jej predchádzajúcu hodnotu, pretože bola použitá v príklade 2 ako vektor. Takéto vynulovanie sa dá zabezpečiť použitím symbolov   =. (bodka):

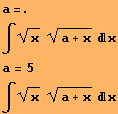
a=. ∫x^(1/2) (a + x)^(1/2) x a = 5 ∫x^(1/2) (a + x)^(1/2) x

(a + x)^(1/2) ((a x^(1/2))/4 + x^(3/2)/2) - 1/4 a^2 Log[x^(1/2) + (a + x)^(1/2)]

5

(5 + x)^(1/2) ((5 x^(1/2))/4 + x^(3/2)/2) - 25/4 ArcSinh[x^(1/2)/5^(1/2)]

Príklad 9. Zobrazme na intervale [0, 1] graf funkcie  f= x^(1/2) (a + x)^(1/2), ktorá bola integrandom v predchádzajúcom príklade, pričom nech sa napr. а = 5.

f = x^(1/2) (a + x)^(1/2) Plot[f, {x, 0, 1}]

x^(1/2) (5 + x)^(1/2)

[Graphics:HTMLFiles/index_38.gif]

⁃Graphics⁃

Príklad 10. Vypočítajme integrál tej istej funkcie na intervale [0,1] pre a = 7.  Pridaním symbolu ; (bodkočiarka) dosiahneme, že hodnota premennej a sa nezobrazí .

a = 7 ; ∫_0^1x^(1/2) (a + x)^(1/2) x RowBox[{RowBox[{∫_0, ^, 1.}], x^(1/2) (a + x)^(1/2) x}]

9/2^(1/2) - 49/4 ArcSinh[1/7^(1/2)]

1.8376

Príklad 11. Zobrazme grafy funkcií sin (2.5x) + cot (x)   na intervale [-3π, 2π], kde cot[x] je funkcia kotangens. V druhom grafe ohraničíme zobrazované hodnoty funkcie na interval medzi -2 a 2. Zobrazujú sa aj vertikálne asymptoty grafu funkcií.

RowBox[{Plot, [, RowBox[{RowBox[{RowBox[{Sin, [, RowBox[{2.5, x}], ]}], +, Cot[x]}], ,, {x, -3 ... ox[{2.5, x}], ]}], +, Cot[x]}], ,, {x, -3π, 2π}, ,, , PlotRange {-2, 2}}], ]}]

[Graphics:HTMLFiles/index_44.gif]

⁃Graphics⁃

[Graphics:HTMLFiles/index_46.gif]

⁃Graphics⁃

Príklad 12. V jednom obrázku môžeme zobraziť grafy viacerých funkcií:

f1 = ArcSin[2x] f2 = ArcCos[x] RowBox[{Plot, [, RowBox[{{f1, f2}, ,, , RowBox[{{, RowBox[{x, ,, RowBox[{-, 0.5}], ,, , 0.5}], }}]}], ]}]

ArcSin[2 x]

ArcCos[x]

[Graphics:HTMLFiles/index_51.gif]

⁃Graphics⁃

Príklad 13. Príkladom 3D grafiky je zobrazenie grafu funkcie dvoch premenných v karteziánskej súradnicovej sústave. Hranice intervalov pre jednotlivé premenné treba zvoliť rozumne, aby sa v bodoch určenej oblasti dala vyjadriť hodnota funkcie. Pridaný je aj parameter špecifikujúci počet bodov zobrazovanej mriežky v oboch smeroch, teda hustotu grafu.

Plot3D[Sin[(x^3 * y)/(x + 2y)], {x, π/2, π}, {y, 0, π}, PlotPoints40]

[Graphics:HTMLFiles/index_54.gif]

⁃SurfaceGraphics⁃

Príklad 14. Iným príkladom 3D grafiky je graf funkcie, ktorá nie je definovaná pre hodnoty premennej y = 0. Systém Mathematica sa snaží nakresliť spojitý graf funkcie, a obe časti grafu danej nespojitej funkcie spojí časťou roviny.

RowBox[{Plot3D, [, RowBox[{RowBox[{RowBox[{Sin, [, RowBox[{2.5, x}], ]}], +, Cot[ y]}], ,, {x, -π, π}, ,, {y, -π/2, π/2}}], ]}]

[Graphics:HTMLFiles/index_57.gif]

⁃SurfaceGraphics⁃

Created by Mathematica  (October 6, 2007)