Metóda najmenších štvorcov pre aproximáciu dát pomocou systému Mathematica
Základy
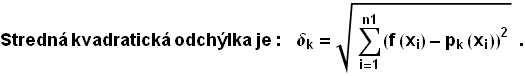
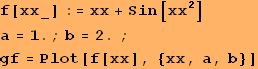
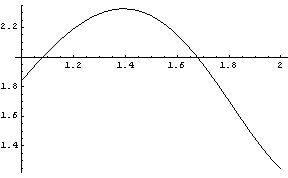
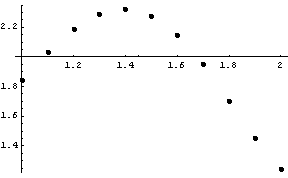
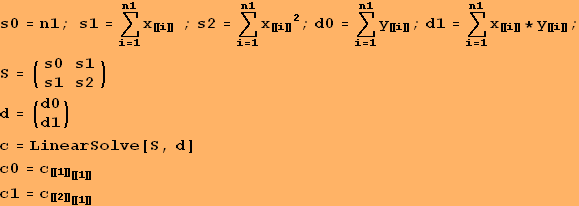
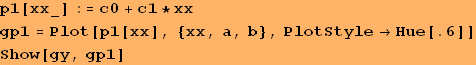
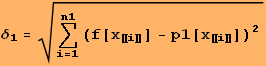
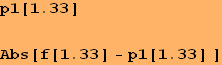
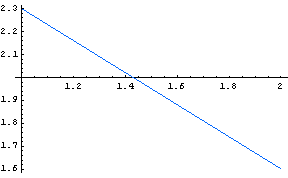
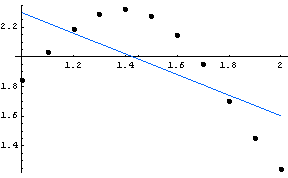
Záver: Vypočítaná chyba 
je evidentne veľká a je zrejmá aj zo zobrazených grafov oboch funkcií. Je preto potrebné nájsť aproximáciu polynómom vyššieho stupňa.
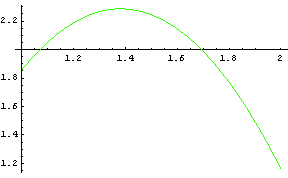
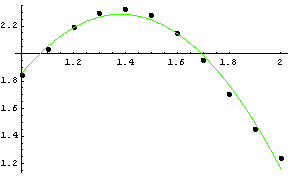
Príklad 2. Vrátime sa k funkcii z predchádzajúceho príkladu 1: a) Nájdeme polynóm druhého stupňa, ktorý je najlepšou aproximáciou pomocou LSM. b) Vyhodnotíme chybu aproximácie. c) Nájdeme približnú hodnotu f(1.33).
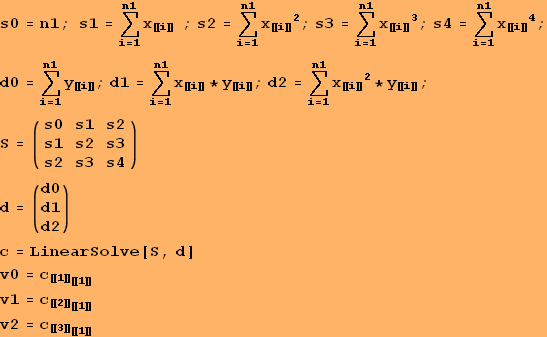
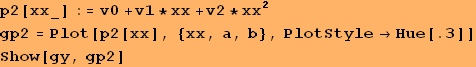
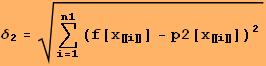
Záver: Získané chyby 
a aer asú evidentne ešte stále veľké, ale akceptovateľnejšie, ako v predchádzajúcej aproximácii (porovnajte aj grafy oboch funkcií). Nájdeme preto aproximáciu polynómom ešte vyššieho stupňa.
Príklad 3. Opäť sa vrátime k funkcii z príkladu 1: a) Nájdeme aproximačný polynóm piateho stupňa .b) Vyhodnotíme chybu aproximácie. c) Nájdeme približnú hodnotu funkcie f(1.33).
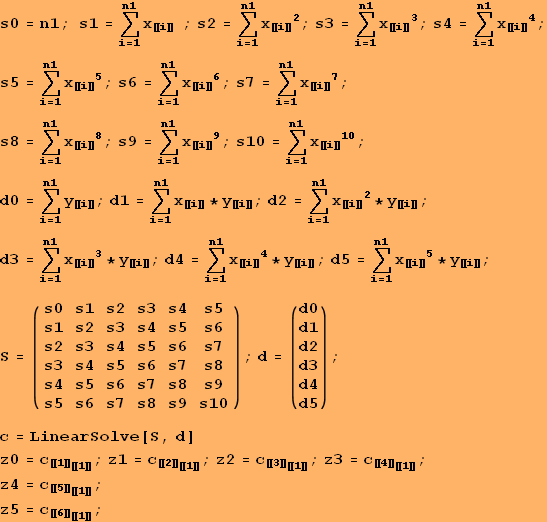
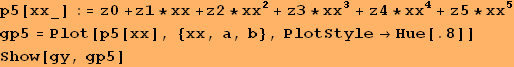
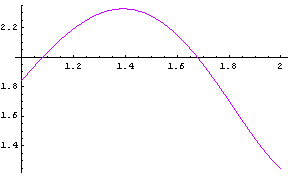
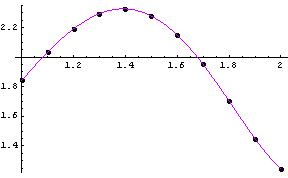
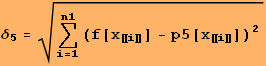
Záver: Získaná chyba 
a absolútna chyba majú pomerne vyhovujúce hodnoty.
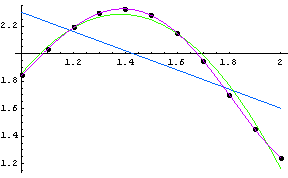
Príklad 4. Zobrazte riešenia predchádzajúcich troch príkladov v jednom grafe.
